How to Calculate Standard Deviation if You Know the Variance

Standard Deviation and Variance

Deviation just ways how far from the normal

Standard Divergence

The Standard Difference is a mensurate of how spread out numbers are.

Its symbol is σ (the greek letter sigma)

The formula is piece of cake: it is the square root of the Variance. And then now yous ask, "What is the Variance?"

Variance

The Variance is defined as:

The boilerplate of the squared differences from the Mean.

To calculate the variance follow these steps:

• Work out the Mean (the simple average of the numbers)
• And so for each number: subtract the Mean and square the result (the squared difference).
• Then piece of work out the average of those squared differences. (Why Square?)

Instance

Yous and your friends accept just measured the heights of your dogs (in millimeters):

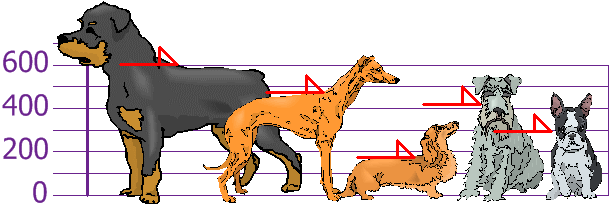
The heights (at the shoulders) are: 600mm, 470mm, 170mm, 430mm and 300mm.

Find out the Mean, the Variance, and the Standard Divergence.

Your first pace is to find the Hateful:

Answer:

Mean	=	600 + 470 + 170 + 430 + 300 v
	=	1970 v
	=	394

so the mean (average) elevation is 394 mm. Allow's plot this on the nautical chart:

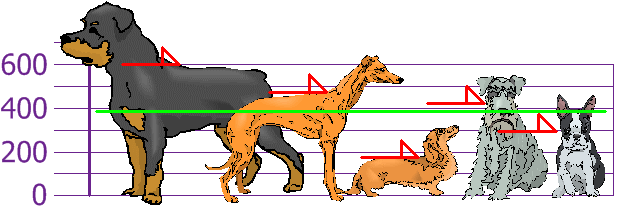
Now we summate each domestic dog's difference from the Hateful:

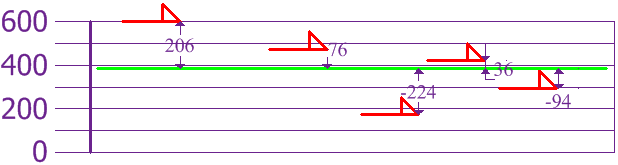
To summate the Variance, take each divergence, square it, and and so average the issue:

Variance
σtwo	=	2062 + 762 + (−224)2 + 362 + (−94)2 5
	=	42436 + 5776 + 50176 + 1296 + 8836 5
	=	108520 5
	=	21704

And so the Variance is 21,704

And the Standard Deviation is simply the square root of Variance, so:

Standard Departure
σ	=	√21704
	=	147.32...
	=	147 (to the nearest mm)

And the good thing about the Standard Deviation is that it is useful. At present we tin can show which heights are within one Standard Departure (147mm) of the Mean:

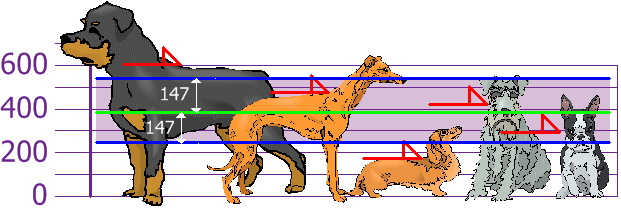
So, using the Standard Difference nosotros have a "standard" way of knowing what is normal, and what is actress large or extra small.

Rottweilers are tall dogs. And Dachshunds are a chip brusk, correct?

Using

We can expect about 68% of values to be within plus-or-minus 1 standard deviation.

Read Standard Normal Distribution to learn more.

Besides try the Standard Deviation Calculator.

Simply ... there is a small change with Sample Data

Our example has been for a Population (the five dogs are the only dogs we are interested in).

Simply if the data is a Sample (a selection taken from a bigger Population), then the calculation changes!

When you take "N" data values that are:

• The Population: divide by Due north when calculating Variance (like we did)
• A Sample: divide by N-i when computing Variance

All other calculations stay the aforementioned, including how we calculated the mean.

Example: if our v dogs are just a sample of a bigger population of dogs, nosotros divide by iv instead of 5 like this:

Sample Variance = 108,520 / 4 = 27,130

Sample Standard Deviation = √27,130 = 165 (to the nearest mm)

Remember of it as a "correction" when your data is only a sample.

Formulas

Here are the ii formulas, explained at Standard Difference Formulas if yous want to know more:

The "Population Standard Deviation":
The "Sample Standard Deviation":

Looks complicated, but the of import change is to
divide past N-ane (instead of N) when calculating a Sample Standard Deviation.

*Footnote: Why square the differences?

If nosotros merely add together up the differences from the mean ... the negatives cancel the positives:

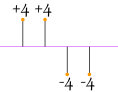four + four − 4 − 4 4 = 0

So that won't work. How about nosotros use absolute values?

|4| + |4| + |−4| + |−4| four = four + iv + four + 4 iv = four

That looks good (and is the Mean Deviation), merely what nearly this case:

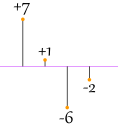|7| + |one| + |−6| + |−2| 4 = seven + 1 + 6 + two four = 4

Oh No! It too gives a value of 4, Even though the differences are more spread out.

And then let united states of america endeavor squaring each deviation (and taking the square root at the end):

That is nice! The Standard Deviation is bigger when the differences are more spread out ... simply what we desire.

In fact this method is a similar idea to altitude between points, but applied in a different way.

And information technology is easier to use algebra on squares and square roots than absolute values, which makes the standard deviation easy to employ in other areas of mathematics.

Return to Top

699, 1472, 1473, 3068, 3069, 3070, 3071, 1474, 3804, 3805

marshwhoulet.blogspot.com

Source: https://www.mathsisfun.com/data/standard-deviation.html

Share this post